Running on Empty?
Basic Sensor Sense (Continued)
by Paul Figie
Automation Engineer
EZAutomation
 In the process control environment there will be tanks to be filled and emptied knowing how much is in your tank can be critical. Aside from point level sensors high, mid, and low level in this article we are going to cover different techniques to more precisely determine the amount of product stored in a tank.
In the process control environment there will be tanks to be filled and emptied knowing how much is in your tank can be critical. Aside from point level sensors high, mid, and low level in this article we are going to cover different techniques to more precisely determine the amount of product stored in a tank.
What’s in your Tank? The type of material in your tank is a very important part in determining how it is going to be measured. Solids like Plastic resin pellets, Powders or grains will be different from Liquids and slurries.
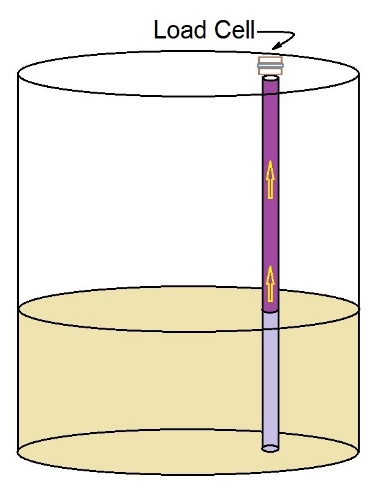
 What would seem to be the simplest method is to just place load cells under the tank legs and weigh the tank with its contents and subtract the empty tank weight. Things to take into account are all attached piping must be flexible so the weight readings will be made accurately and any vibration is isolated so it will not interfere with the load cell readings.
What would seem to be the simplest method is to just place load cells under the tank legs and weigh the tank with its contents and subtract the empty tank weight. Things to take into account are all attached piping must be flexible so the weight readings will be made accurately and any vibration is isolated so it will not interfere with the load cell readings.
In some cases it is not practical or possible to use this type of load cell method.
Gravity displacement method uses a long cylindrical material acting like a float that will place pressure on a load cell inside the tank at the very top. As the tank fills the displaced pressure on the load cell increases allowing the tank fill to be calculated. Care has to be taken that the float cylinder will place an accurate force on the load cell and that it moves freely but remains in alignment with the load cell. The specific gravity of the float cylinder and the product filling the tank are used to calculate the fill level.
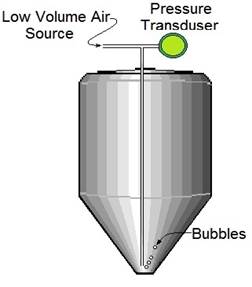 The next method that is my preferred for liquids is to place a differential pressure transducer at the lowest fill point of the tank with a measurement range of water column equal to height of the tank. Another version of this method that keeps the liquid from contacting the pressure transducer commonly called a bubbler places a low volume air source to a tube with its outlet at the lowest fill point of the tank as the tank fills the pressure to release the bubble increases. The Bubbler method maybe necessary for slurries that may clog transducer ports or highly corrosive liquids that could cause damage to the pressure transducer.
The next method that is my preferred for liquids is to place a differential pressure transducer at the lowest fill point of the tank with a measurement range of water column equal to height of the tank. Another version of this method that keeps the liquid from contacting the pressure transducer commonly called a bubbler places a low volume air source to a tube with its outlet at the lowest fill point of the tank as the tank fills the pressure to release the bubble increases. The Bubbler method maybe necessary for slurries that may clog transducer ports or highly corrosive liquids that could cause damage to the pressure transducer.
For measuring Liquids these techniques that have been used very effectively.
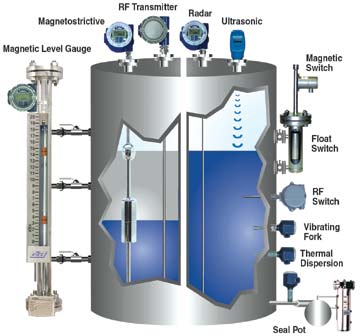
Now that we have covered the major Gravity/Weight methods I will list some of the others that could be used for your application: Noncontact distance measurement can be used with Ultrasonic or Radar sensors these types may be the only way to measure very low density materials. By measuring the distance from the top of the tank to the level of the material the fill volumes can then be calculated based on the shape and dimensions of the tank. When the materials are Bulk solids such as Grains, Powders, or Pellets are stored filling and drawing product from your tank will leave a cone shape in the material depending on the consistency. Taking in to consideration the product that is being filled and its physical properties will be critical in selecting the best measuring process.
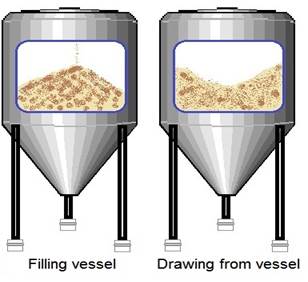 RF probes and magnostrictive technologies can also be used to give a distance measurements to calculate you tank fill these types do come in contact with the material being sensed. In most cases having additional High and low level point sensors as redundancy and a safety measure is always a good idea.
RF probes and magnostrictive technologies can also be used to give a distance measurements to calculate you tank fill these types do come in contact with the material being sensed. In most cases having additional High and low level point sensors as redundancy and a safety measure is always a good idea.
Transducers have a wide variety of output forms some of the more common are 0-5Vdc 0-10Vdc and 4-20ma these signals will be the raw input to your PLC or device and will be converted to a digital signal (Analog to Digital) depending on the span or range of your transducer and the accuracy of what your process requires a suitable Analog input card should be selected. Standard Analog inputs are 12bit (0-4096) and on the EZRack PLC a high resolution 16Bit (0-65535) Analog card is available giving incredible accuracy.
Everything you need to calculate volume in a Tank to obtain fill levels
One Gallon or Water = 0.133680556 Cubic Foot & One Cubic Foot will hold 7.48052 Gallons
One inch of Water column is equal to 0.036091 PSI
- Tank Must be vented to Atmosphere
- With an Absolute Pressure transduced Atmosphere pressure must be accounted for
- With a Differential Pressure transducer Atmosphere pressure is compensated
- Pressure transducer must sense at the bottom level with level of the empty tank. (Example 12” below will add 12” water column)
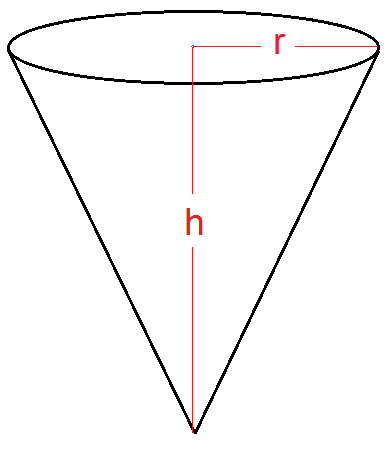 Cone End Volume formula
Cone End Volume formula
Volume = 1/3 * h * π* r2
Horizontal Cylinder Tank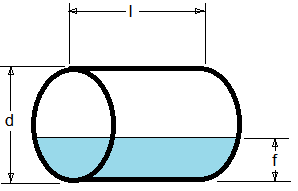
Total volume of a cylinder shaped tank is the area, A, of the circular end times the length, l. A = πr2 where r is the radius which is equal to 1/2 the diameter or d/2. Therefore:
V(tank) = πr2l
Calculate the filled volume of a horizontal cylinder tank by first finding the area, A, of a circular segment and multiplying it by the length, l.
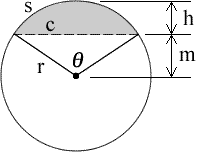 Area of the circular segment, the grey shaded area, is A = (1/2)r2(θ - sinθ) where θ = 2*arccos(m/r) and θ is in radians. Therefore, V(segment) = (1/2)r2(θ - sinθ)l. If the fill height f is less than 1/2 of d then we use the segment created from the filled height and V(fill) = V(segment). However, if the fill height f is greater than 1/2 of d then we use the segment that is created by the empty portion of the tank and subtract it from the total volume to get the filled volume; V(fill) = V(tank) - V(segment).
Area of the circular segment, the grey shaded area, is A = (1/2)r2(θ - sinθ) where θ = 2*arccos(m/r) and θ is in radians. Therefore, V(segment) = (1/2)r2(θ - sinθ)l. If the fill height f is less than 1/2 of d then we use the segment created from the filled height and V(fill) = V(segment). However, if the fill height f is greater than 1/2 of d then we use the segment that is created by the empty portion of the tank and subtract it from the total volume to get the filled volume; V(fill) = V(tank) - V(segment).
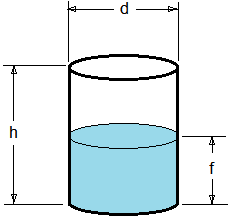
Vertical Cylinder Tank
Total volume of a cylinder shaped tank is the area, A, of the circular end times the height, h. A = πr2 where r is the radius which is equal to d/2. Therefore:
V(tank) = πr2h
The filled volume of a vertical cylinder tank is just a shorter cylinder with the same radius, r, and diameter, d, but height is now the fill height or f. Therefore:
V(fill) = πr2f
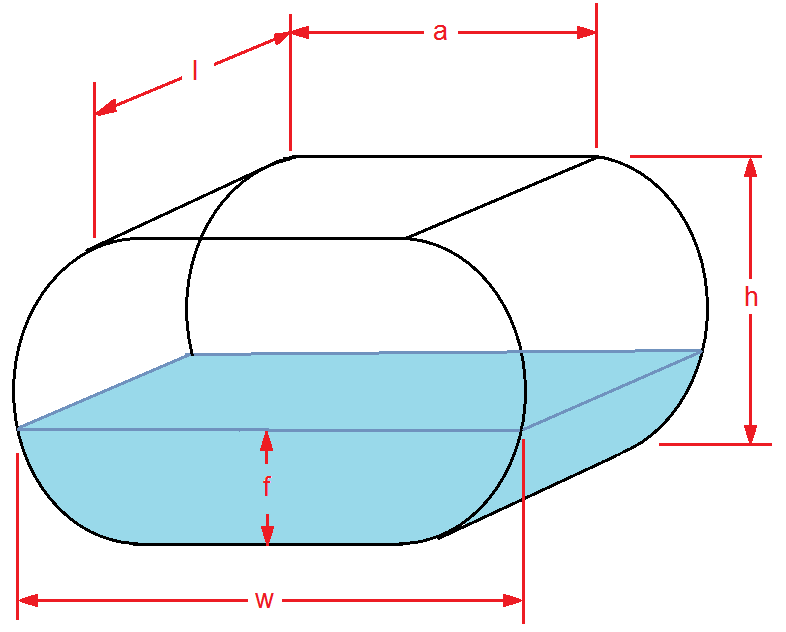
Horizontal Oval Tank
 Volume of an oval tank is calculated by finding the area, A, of the end, which is the shape of an elongated circle, and multiplying it by the length, l. A = πr2 + 2ra and it can be proven that r = h/2 and a = w - h where w>h must always be true. Therefore:
Volume of an oval tank is calculated by finding the area, A, of the end, which is the shape of an elongated circle, and multiplying it by the length, l. A = πr2 + 2ra and it can be proven that r = h/2 and a = w - h where w>h must always be true. Therefore:
V(tank) = (πr2 + 2ra)l
Volume of fill of a horizontal oval tank is best calculated if we assume it is 2 halves of a cylinder separated by a rectangular tank. We then calculate fill volume of 1) a Horizontal Cylinder Tank where l = l, f = f, and diameter d = h, and 2) a Rectangle Tank where l = l, f = f, and rectangle width w is a = w - h of the oval tank.
V(fill) = V(fill-horizontal-cylinder) + V(fill-rectangle)
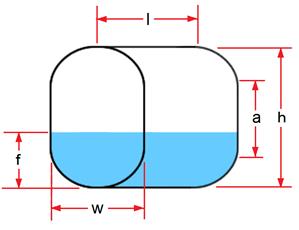
Vertical Oval Tank
 To calculate volume of an oval tank find the area, A, of the end, which is the shape of an elongated circle, and multiply it by the length, l. A = πr2 + 2ra and it can be proven that r = w/2 and a = h - w where h>w must always be true. Therefore:
To calculate volume of an oval tank find the area, A, of the end, which is the shape of an elongated circle, and multiply it by the length, l. A = πr2 + 2ra and it can be proven that r = w/2 and a = h - w where h>w must always be true. Therefore:
V(tank) = (πr2 + 2ra)l
To calculate fill volume of a vertical oval tank it is best if we assume it is 2 halves of a cylinder separated by a rectangular tank. With r = w/2 = height of the semicircle ends, we can define 3 general fill position areas.
- Fill, f < r
We calculate fill volume using the circular segment method, as in a Horizontal Cylinder Tank, for the filled portion.
- Fill, f > r and f < (r+a)
The filled volume is exactly 1/2 of the cylinder portion plus the volume of fill inside the rectangular portion.
- Fill, f > (r+a) and f < h
We calculate fill volume using the circular segment method, as in a Horizontal Cylinder Tank, for the empty portion. Volume will be V(tank) - V(segment).
Horizontal Capsule Tank
 We treat a capsule as a sphere of diameter d split in half and separated by a cylinder of diameter d and height a. Where r = d/2.
We treat a capsule as a sphere of diameter d split in half and separated by a cylinder of diameter d and height a. Where r = d/2.
V(sphere) = (4/3)πr3, and
V(cylinder) = πr2a, therefore
V(capsule) = πr2((4/3)r + a)
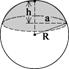 Volume of fill for a horizontal capsule is done by using the circular segment method for the Horizontal Cylinder and, with a similar approach, using calculations of a spherical cap for the sphere section of the tank where,
Volume of fill for a horizontal capsule is done by using the circular segment method for the Horizontal Cylinder and, with a similar approach, using calculations of a spherical cap for the sphere section of the tank where,
V(spherical cap) = (1/3)πh2(3R - h)
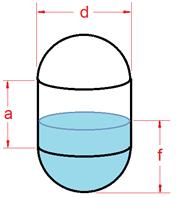
Vertical Capsule Tank
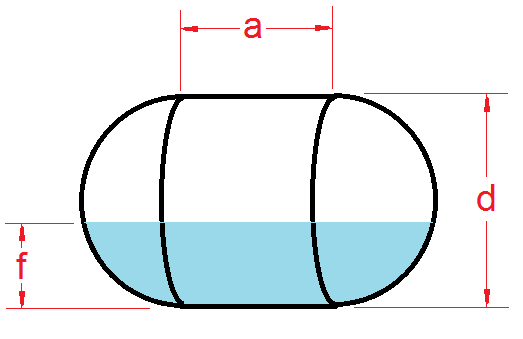 To calculate the volume of a vertical capsule tank treat the capsule as a sphere of diameter d split in half and separated by a cylinder of diameter d and height a. Where r = d/2.
To calculate the volume of a vertical capsule tank treat the capsule as a sphere of diameter d split in half and separated by a cylinder of diameter d and height a. Where r = d/2.
V(capsule) = πr2((4/3)r + a)
To calculate fill volume of a vertical capsule calculate in a fashion similar to the method used for the Vertical Oval Tank where r = d/2 = height of each hemisphere end.
- Fill, f < r
We calculate fill volume using the spherical cap method, for the filled portion.
- Fill, f > r and f < (r+a)
The filled volume is exactly 1/2 of the sphere portion plus the volume of fill inside the vertical cylinder portion.
- Fill, f > (r+a) and f < h
We calculate fill volume using the spherical cap method for the empty portion. Volume will be V(tank) - V(spherical cap).